On reprend ici
des énigmes
proposées en exercice dans les pages 'if'.
Le roi cruel.
Un roi cruel avait pour habitude de proposer le marché suivant à ses condamnés :
- Tout prisonnier doit choisir entre deux cellules. Chaque cellule peut contenir une corde ou une clef (un seul objet par cellule).
-
Si le prisonnier choisit une cellule avec corde, il sera pendu.
-
Si le prisonnier choisit une cellule avec clef, il sera libéré.
Les cellules contiennent parfois toutes deux une corde ou parfois toutes deux une clef. Parfois l'une contient une clef et l'autre une corde.
Un condamné se présente devant les deux cellules.
- Sur la porte de la cellule 1 est inscrite l'affirmation A1 suivante : " il y une clef dans cette cellule et une corde dans la cellule d'à côté."
- Sur la porte de la cellule 2 est inscrite l'affirmation A2 suivante : "il y a une clef dans l'une des cellules et une corde dans l'autre."
Le roi, magnanime, donne une indication (exacte) au prisonnier : "Seule l'une des deux portes porte une indication vraie."
Vous saurez, sans doute, mener le raisonnement simple permettant de découvrir la porte conduisant à la liberté. Mais
l'objectif de l'exercice est de monter un circuit (avec logisim) donnant la réponse.
- On note
- L1 : " la cellule 1 contient une clef."
- L2 : "la cellule 2 contient une clef."
Traduire les affirmations A1 et A2 à l'aide des propositions L1 et L2 et des connecteurs logiques et, ou, non.
- Monter un circuit, d'entrées L1 et L2, et indiquant en sortie le choix que doit faire le condamné.
Expression de A1 et A2
A1 = L1 et non(L2)
A2 = ( L1 et non(L2) ) ou ( non(L1) et L2 )
Et l'indication du roi nous assure que A1 xor A2 = true.
Schéma
Le schéma logisim à charger
montre que la sortie ne s'allume que pour L1=0 et L2=1.
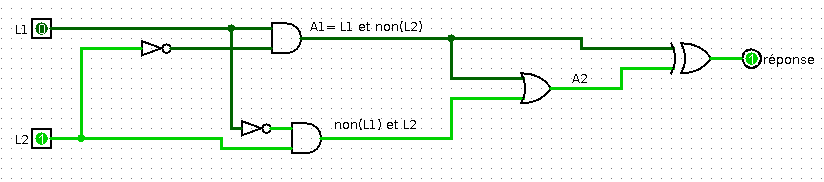
Le prisonnier doit donc choisir d'ouvrir la porte 2.
Le retour du roi cruel.
On retrouve notre roi cruel.
Un condamné se présente devant les deux cellules.
- Sur la porte de la cellule 1 est inscrite l'affirmation A1 suivante : "Au moins l'une des deux cellules contient une clef."
- Sur la porte de la cellule 2 est inscrite l'affirmation A2 suivante : "L'autre cellule contient une corde."
Le roi, magnanime, donne une indication (exacte) au prisonnier : "Les deux inscriptions sont soit toutes deux vraies, soient toutes deux fausses."
Déterminer la réponse à donner en suivant la démarche de l'exercice précédent.
A1 = L1 or L2
A2 = not(L1)
L'indication du roi se traduit par ( non(A1) et non(A2) ) ou ( A1 et A2 ) = true, ou encore non (A1 xor A2) = true,
d'où l'utilisation d'une porte xnor (porte non xor).
Le schéma logisim à charger montre que la sortie n'est à 1
que lorsque L1=0 et L2=1.

Le prisonnier doit donc choisir la porte 2.
Politiques et naïfs.
Dans un pays, il y a deux sortes d'habitants :
- Les politiques, qui mentent toujours.
- Les naïfs, qui disent toujours la vérité.
Je croise deux habitants A et B.
A affirme : "Au moins l'un de nous deux est un politique."
On note :
- a : " A est naïf. "
- b : " B est naïf. "
Déterminer un circuit permettant d'identifier la nature de A et B.
La phrase prononcée par A est : "not(a) or not(b)".
On ajoute que la valeur de vérité de cette phrase doit être en accord avec la nature de A :
- Si A est naïf, la phrase est vraie.
- Si A est politique, la phrase est fausse.
En d'autres termes ( a and phrase_de_A ) or ( not(a) and not(phrase_de_A) ) doit valoir True,
ce qui s'écrit aussi a xnor phrase_de_A = true.
Le schéma logisim à charger montre que la sortie n'est à 1
que lorsque a=1 et b=0.
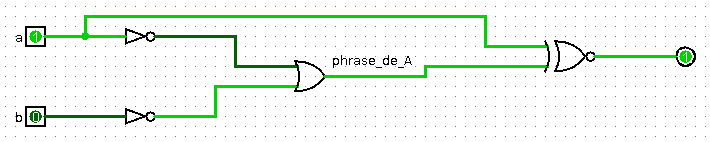
A est donc un naïf et B un politique.
Politiques et naïfs (2).
Un peu plus loin, je croise deux autres personnes A et B.
A affirme : "Je suis politicien ou B est naïf."
Déterminer les qualités de A et B à l'aide d'une démarche analogue à celle utilisée dans l'exercice précédent.
On note :
- a : " A est naïf. "
- b : " B est naïf. "
La phrase prononcée par A est : "not(a) or b".
On ajoute que la valeur de vérité de cette phrase doit être en accord avec la nature de A :
- Si A est naïf, la phrase est vraie.
- Si A est politique, la phrase est fausse.
En d'autres termes ( a and phrase_de_A ) or ( not(a) and not(phrase_de_A) ) doit valoir True.
ce qui s'écrit aussi a xnor phrase_de_A = true.
Le schéma logisim à charger ci-dessous montre que la sortie n'est à 1
que lorsque a=1 et b=1.
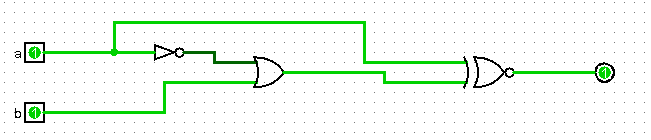
A et B sont donc tous deux naïfs.



