NOT.
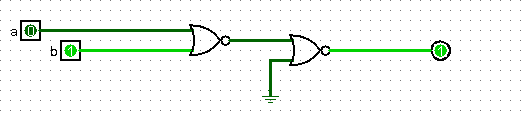
Monter l'équivalent d'une porte NOT en utilisant uniquement des portes NOR. Tester avec logisim.
On note \( \mathbb{B}\) l'ensemble \( \lbrace 0 ; 1 \rbrace \) (que l'on peut considérer suivant la situation comme l'ensemble { vrai ; faux } ).
Toute fonction définie sur \( \mathbb{B}^n \) et à valeurs dans \( \mathbb{B} \) peut être exprimée à l'aide de la seule fonction définie sur \( \mathbb{B}^2\) par nor(a,b) = non (a ou b).
On note parfois nor (a,b) par \( a \downarrow b \).
L'objectif des exercices de cette page est de traduire not, et, ou en circuits logiques n'utilisant que les portes nor.
Le schéma logisim à charger
utilise l'idée simple suivante : non(a) = non( a ou a) = nor( a, a)= \( a \downarrow a \).
On peut aussi remarquer que non(a) = non( a ou 0 ) = nor(a,0) = \( a \downarrow 0 \)
comme sur le schéma à charger ici.
AND.
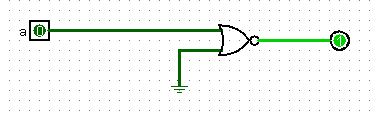
Monter l'équivalent d'une porte AND en utilisant uniquement des portes NOR. Tester avec logisim.
Le schéma logisim à charger
utilise l'idée suivante :
a et b = non(non( a et b )) = non ( non(a) ou non(b) )= \( \text{non}(a) \downarrow \text{non}(b) \).
Et nous venons d'exprimer la porte non à l'aide d'une porte nor :
a et b = \( (a\downarrow a) \downarrow (b\downarrow b) \) (premier schéma)
ou encore a et b = \( (a\downarrow 0) \downarrow (b\downarrow 0) \) (second schéma).
OR.
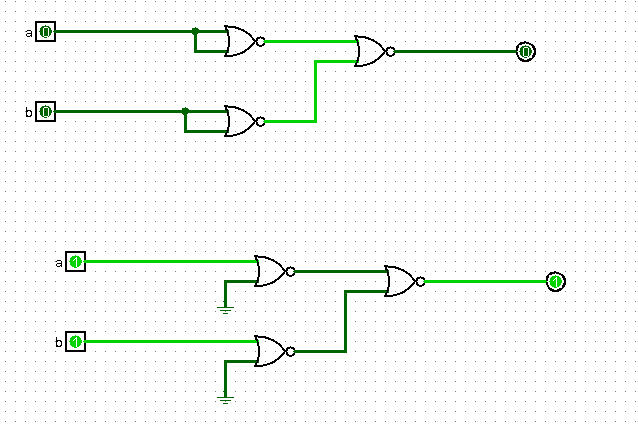
Monter l'équivalent d'une porte OR en utilisant uniquement des portes NOR. Tester avec logisim.
Le schéma logisim à charger
utilise l'idée suivante :
a ou b = non(non( a ou b )) = non ( \( a \downarrow b \) )= \( (a \downarrow b) \downarrow 0 \).
