De Morgan.
Les formules de De Morgan doivent être connues.
Elles s'énoncent ainsi :
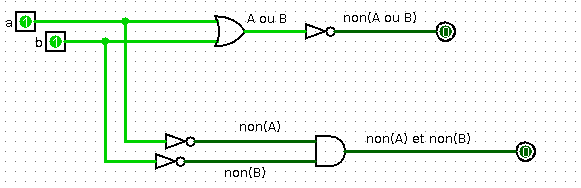
- non(A ou B) = non(A) et non(B)
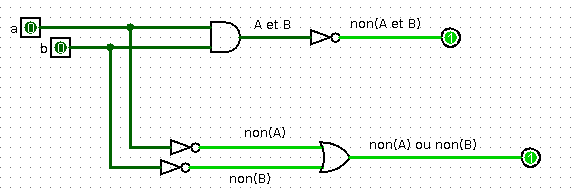
- non( A et B) = non(A) ou non(B)
Illustrer et vérifier ces formules à l'aide de circuits logisim.
L'objectif de cette page est d'illustrer par des circuits logisim des formules de logique importantes à connaître.
Les tests sur ce schéma logisim à charger montrent que les deux sorties sont toujours identiques, ce qui prouve l'égalité non(A et B) = non(A) ou non(B).
Les tests sur ce schéma logisim à charger montrent que les deux sorties sont toujours identiques, ce qui prouve l'égalité non(A ou B) = non(A) et non(B).
Différence symétrique.
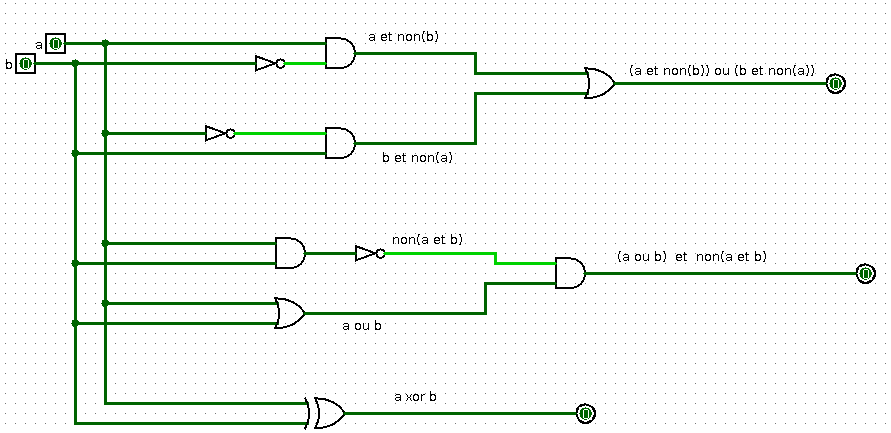
La différence symétrique est plutôt nommée xor en logique.
On a : xor(A, B) = (A et non(B)) ou (B et non(A)) = (A ou B) et non(A et B).
Illustrer et vérifier cette formule à l'aide d'un circuit logisim.
Les tests sur ce schéma logisim à charger
montrent que les trois sorties sont toujours identiques, ce qui prouve les égalités annoncées.
