Réécriture par substitution.
On dispose d'une chaîne de caractères et on la transforme ainsi : chaque lettre F est remplacée par F+F--F+F.
Si ch='FA+-FB', la chaîne obtenue après transformation est donc la chaîne
'F+F--F+FA+-F+F--F+FB'.
Écrire une fonction :
- Entrée : une chaîne de caractères.
- Sortie : la chaîne de caractères transformée suivant le principe précédent.
On pourra ensuite modifier la fonction en ajoutant un paramètre permettant d'appliquer plusieurs fois de suite la transformation.
Une solution possible :
def regle(ch) :
""" règle de substitution
de F par F+F--F+F
dans la chaîne."""
chaineIntermediaire = ''
for carac in ch :
if carac == 'F' :
chaineIntermediaire += 'F+F--F+F'
else :
chaineIntermediaire += carac
return chaineIntermediaire
ch = 'F--F--F'
ch = regle(ch)
print(ch)
On peut aussi utiliser la méthode replace du langage python :
def regle(ch) :
""" règle de substitution
de F par F+F--F+F
dans la chaîne."""
ch=ch.replace('F','F+F--F+F')
return ch
ch = 'F--F--F'
nombre_de_transfo = 2
for _ in range(nombre_de_transfo) :
ch = regle(ch)
print(ch)
En ajoutant le nombre de transformations dans les paramètres de la fonction, cela peut donner :
def regle(ch, nbtransfo) :
""" ch est une chaîne de caractères
Avec nbtransfo = 1, la fonction retourne la chaîne obtenue
en remplaçant F par F+F--F+F dans la chaîne ch.
Avec nbtransfo = 2, la transformation est appliquée à nouveau
à la chaîne regle(chaineInitiale, 1).
Avec nbtransfo = 3, la transformation est appliquée à nouveau
à la chaîne regle(chaineInitiale, 2)...
"""
for _ in range(nbtransfo) :
ch = ch.replace('F','F+F--F+F')
return ch
print( regle(ch = 'F--F--F', nbtransfo = 2) )
Le flocon de Von Koch.
On reprend la transformation de l'exercice précédent.
On interprète maintenant une chaîne de caractères, en parcourant ses caractères dans l'ordre,
à l'aide d'une tortue de la façon suivante :
- à chaque lettre F, la tortue avance d'une unité de longueur (dans la direction donnée par sa tête, unité à fixer),
- à chaque signe + rencontré, la tortue tourne sur la gauche de 60 degrés,
- à chaque signe - rencontré, la tortue tourne sur la droite de 60 degrés.
On part de la chaîne ch='F--F--F', on transforme cette chaîne un certain nombre de fois suivant le processus
de transformation de l'exercice précédent. Puis on interprète la chaîne finale suivant le principe exposé ci-dessus.
Programmez...
Une première solution
Dans cette première solution, on traduit assez directement les instructions données dans l'énoncé.
from turtle import *
def regle(ch, nbtransfo) :
""" ch est une chaîne de caractères
Avec nbtransfo = 1, la fonction retourne la chaîne obtenue
en remplaçant F par F+F--F+F dans la chaîne ch.
Avec nbtransfo = 2, la transformation est appliquée à nouveau
à la chaîne regle(chaineInitiale, 1).
Avec nbtransfo = 3, la transformation est appliquée à nouveau
à la chaîne regle(chaineInitiale, 2)...
"""
for _ in range(nbtransfo) :
ch = ch.replace('F','F+F--F+F')
return ch
def dessine(ch, unite) :
"""
Interprétation de la chaîne par la tortue.
"""
for x in ch :
if x == 'F' :
forward(unite)
elif x == '+' :
left(60)
elif x == '-' :
right(60)
speed(0) # tortue rapide
dessine( regle(ch = 'F--F--F', nbtransfo = 2) , unite = 10)
hideturtle() # on masque la tortue
mainloop() # maintenir fenêtre ouverte
Avec 2 transformations, on obtient :


Seconde solution
En faisant des essais avec la solution précédente, on se rend compte d'un problème : l'ouverture de la fenêtre.
Une mauvaise ouverture peut conduire à ne voir qu'une partie de la figure, ou même à ne rien voir
de la figure obtenue (soit parce que la figure se trouve trop petite vis à vis de cette fenêtre,
soit parce qu'elle se trouve trop
grande ou parce qu'elle est décentrée...)
Nous réglons ce problème ici en recalculant l'ouverture de la fenêtre au fur et à mesure de l'avancée de la tortue.
Nous utilisons pour cela setworldcoordinates().
from turtle import *
def regle(chaineInitiale, nbtransfo) :
"""
chaineInitiale est une chaîne de caractères
Avec nbtransfo = 1, la fonction retourne la chaîne obtenue
en remplaçant F par F+F--F+F dans la chaîne chaineInitiale.
Avec nbtransfo = 2, la transformation est appliquée à nouveau
à la chaîne regle(chaineInitiale, 1).
Avec nbtransfo = 3, la transformation est appliquée à nouveau
à la chaîne regle(chaineInitiale, 2)...
Avec nbtransfo = n, la transformation est appliquée à nouveau
à la chaîne regle(chaineInitiale, n-1).
"""
for _ in range(nbtransfo) :
chaineInitiale = chaineInitiale.replace('F','F+F--F+F')
return chaineInitiale
def dessine(ch, unite) :
""" interprétation de la chaîne par la tortue."""
# parcours de la chaine de caractères :
for x in ch :
# interprétation du caractère lu :
if x == 'F' :
forward(unite)
elif x == '+' :
left(60)
elif x == '-' :
right(60)
# mise à jour de la fenêtre de tracé :
definitFenetre()
def miseAjourExtremeTortue() :
"""
Met à jour les valeurs min et max des abscisses
et ordonnées prises par la tortue lors de ses pérégrinations.
"""
# min des x de la tortue
# (le min des positions précédentes est enregistré dans tortueExtreme[0],
# on prend le min des positions précédentes et de la position actuelle)
tortueExtreme[0] = min( tortueExtreme[0], position()[0])
# max des x de la tortue :
tortueExtreme[2] = max( tortueExtreme[2], position()[0])
# min des y de la tortue :
tortueExtreme[1] = min( tortueExtreme[1], position()[1])
# max des y de la tortue :
tortueExtreme[3] = max( tortueExtreme[3], position()[1])
def definitFenetre() :
"""
On définit une fenêtre carré de tracé en définissant
son coin inférieur gauche (xmin, ymin)
et son coin supérieur droit (xmax, ymax).
La définition des deux coins du coin est obtenue à l'aide du centre
défini lui-même à partir des positions extrêmes qui ont été prises par la tortue
lors de l'ensemble de ses déplacements.
(La fenêtre est définie carrée plutôt que rectangulaire afin d'éviter
un effet d'écrasement sur une direction.)
"""
miseAjourExtremeTortue()
# coordonnées du centre de la nouvelle fenêtre :
xc = (tortueExtreme[0] + tortueExtreme[2]) * 0.5
yc = (tortueExtreme[1] + tortueExtreme[3]) * 0.5
# delta=max(hauteur, largeur) de la nouvelle fenêtre
# pour définir largeur=hauteur pour la nouvelle fenêtre :
delta = max( tortueExtreme[2] - tortueExtreme[0], tortueExtreme[3] - tortueExtreme[1])
# calcul des coins inférieurs gauche
# et supérieur droit de la nouvelle fenêtre :
delta = delta * 0.5
xmin, ymin = xc -delta, yc -delta
xmax, ymax = xc + delta, yc + delta
# ouverture de la fenêtre sur ces nouveaux paramètres :
setworldcoordinates(xmin, ymin, xmax, ymax)
# liste enregistrant les xmin, ymin, xmax, ymax prises par
# la tortue au cours de ses pérégrinations.
# Cette liste est mise à jour par la fonction miseAjourExtremeTortue()
# après chaque déplacement de la tortue :
tortueExtreme = [ 0, 0, 1, 1]
# fenêtre graphique pour le tracé
# caractérisée par le coin inférieur gauche (xmin, ymin)
# et le coin supérieur droit (xmax, ymax).
# Cette fenêtre est redéfinie après chaque déplacement de la tortue
# à l'aide de la fonction definitFenetre().
definitFenetre()
speed(0) # tortue rapide
dessine( regle(chaineInitiale = 'F--F--F', nbtransfo = 3), unite = 1 )
hideturtle() # on masque la tortue
mainloop() # maintenir fenêtre ouverte
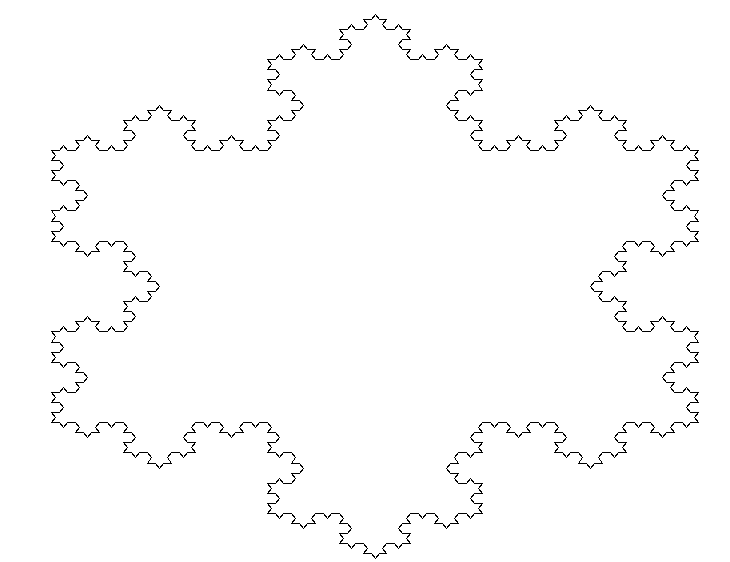
Les figures obtenues constituent les premières étapes de la construction du flocon de Von Koch, fractale pour laquelle
vous trouverez sur le web de nombreuses références.
Vous trouverez sur le principe utilisé ici (L-system) des renseignements et notamment son utilisation pour
la représentation de végétaux sur cette page et
particulièrement dans ce pdf.
Un autre L system.
Cet exercice est très semblable au précédent. Mais on change la règle de transformation de la chaîne et
l'interprétation par la tortue.
On dispose d'une chaîne de caractères et on la transforme ainsi : chaque lettre F est remplacée par FF+F+F+F+F+FF.
On interprète maintenant une chaîne de caractères, en parcourant ses caractères dans l'ordre,
à l'aide d'une tortue de la façon suivante :
- à chaque lettre F, la tortue avance d'une unité (dans la direction donnée par sa tête),
- à chaque signe + rencontré, la tortue tourne sur la gauche de 72 degrés,
- à chaque signe - rencontré, la tortue tourne sur la droite de 72 degrés.
On part de la chaîne ch='F+F+F+F+F', on transforme cette chaîne un certain nombre de fois suivant le processus
de transformation vu plus haut. Puis on interprète la chaîne finale suivant le principe précédent.
Programmez...
Il suffit d'apporter quelques modifications mineures au programme précédent.
from turtle import *
def regle(chaineInitiale, nbtransfo) :
"""
Règle de substitution : F devient FF+F+F+F+F+FF
"""
for _ in range(nbtransfo) :
chaineInitiale = chaineInitiale.replace('F','FF+F+F+F+F+FF')
return chaineInitiale
def dessine(ch, unite, angle) :
""" interprétation de la chaîne par la tortue."""
# parcours de la chaine de caractères :
for x in ch :
# interprétation du caractère lu :
if x == 'F' :
forward(unite)
elif x == '+' :
left(angle)
elif x == '-' :
right(angle)
# mise à jour de la fenêtre de tracé :
definitFenetre()
def miseAjourExtremeTortue() :
"""
Met à jour les valeurs min et max des abscisses
et ordonnées prises par la tortue lors de ses pérégrinations.
"""
# min des x de la tortue
# (le min des positions précédentes est enregistré dans tortueExtreme[0],
# on prend le min des positions précédentes et de la position actuelle)
tortueExtreme[0] = min( tortueExtreme[0], position()[0])
# max des x de la tortue :
tortueExtreme[2] = max( tortueExtreme[2], position()[0])
# min des y de la tortue :
tortueExtreme[1] = min( tortueExtreme[1], position()[1])
# max des y de la tortue :
tortueExtreme[3] = max( tortueExtreme[3], position()[1])
def definitFenetre() :
"""
On définit une fenêtre carré de tracé en définissant
son coin inférieur gauche (xmin, ymin)
et son coin supérieur droit (xmax, ymax).
La définition des deux coins du coin est obtenue à l'aide du centre
défini lui-même à partir des positions extrêmes qui ont été prises par la tortue
lors de l'ensemble de ses déplacements.
(La fenêtre est définie carrée plutôt que rectangulaire afin d'éviter
un effet d'écrasement sur une direction.)
"""
miseAjourExtremeTortue()
# coordonnées du centre de la nouvelle fenêtre :
xc = (tortueExtreme[0] + tortueExtreme[2]) * 0.5
yc = (tortueExtreme[1] + tortueExtreme[3]) * 0.5
# delta=max(hauteur, largeur) de la nouvelle fenêtre
# pour définir largeur=hauteur pour la nouvelle fenêtre :
delta = max( tortueExtreme[2] - tortueExtreme[0], tortueExtreme[3] - tortueExtreme[1])
# calcul des coins inférieurs gauche
# et supérieur droit de la nouvelle fenêtre :
delta = delta * 0.5
xmin, ymin = xc -delta, yc -delta
xmax, ymax = xc + delta, yc + delta
# ouverture de la fenêtre sur ces nouveaux paramètres :
setworldcoordinates(xmin, ymin, xmax, ymax)
# liste enregistrant les xmin, ymin, xmax, ymax prises par
# la tortue au cours de ses pérégrinations.
# Cette liste est mise à jour par la fonction miseAjourExtremeTortue()
# après chaque déplacement de la tortue :
tortueExtreme = [ 0, 0, 1, 1]
# fenêtre graphique pour le tracé
# caractérisée par le coin inférieur gauche (xmin, ymin)
# et le coin supérieur droit (xmax, ymax).
# Cette fenêtre est redéfinie après chaque déplacement de la tortue
# à l'aide de la fonction definitFenetre().
definitFenetre()
speed(0) # tortue rapide
dessine( regle(chaineInitiale = 'F+F+F+F+F', nbtransfo = 3), unite = 1, angle = 72 )
hideturtle() # on masque la tortue
mainloop() # maintenir fenêtre ouverte
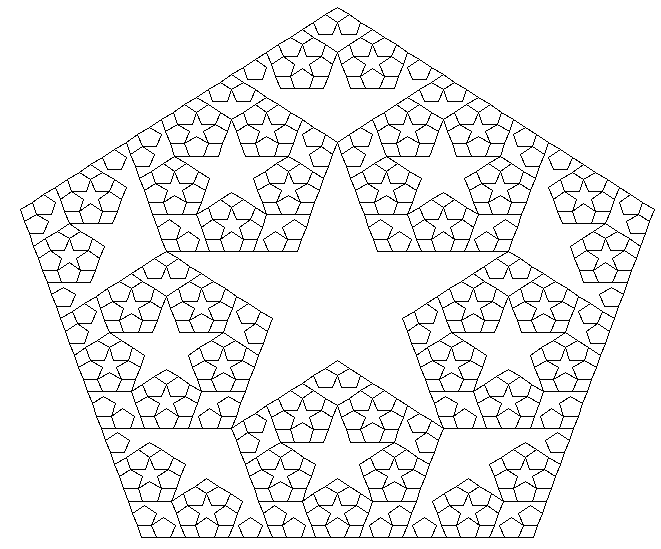
Une plante L system.
On reprend le principe des L-system expliqué dans les exercices précédents.
On dispose d'une chaîne de caractères et on la transforme ainsi : chaque lettre F est remplacée par F[+F]F[-F]F.
On interprète maintenant une chaîne de caractères, en parcourant ses caractères dans l'ordre,
à l'aide d'une tortue de la façon suivante :
- à chaque lettre F, la tortue avance d'une unité (dans la direction donnée par sa tête),
- à chaque signe + rencontré, la tortue tourne sur la gauche de 30 degrés,
- à chaque signe - rencontré, la tortue tourne sur la droite de 30 degrés.
- à chaque symbole [ rencontré, la position (coordonnées+orientation de la tête) de la tortue est empilée.
- à chaque symbole ] rencontré, la position de la tortue est dépilée.
On révisera, si nécessaire, la notion de pile.
On utilise heading() pour connaître et empiler l'orientation de la tortue et position() pour sa position.
Pour se replacer à une position enregistrée, on utilisera setposition() et pour réorienter la tortue dans une direction enregistrée, on utilisera
setheading().
On part de la chaîne ch='F', on transforme cette chaîne un certain nombre de fois suivant le processus
de transformation exposé. Puis on interprète la chaîne finale suivant le principe précédent.
Programmez...
On apporte quelques modifications mineures au programme précédent et on ajoute les fonctions permettant
d'empiler et de dépiler la position de la tortue.
from turtle import *
# liste servant de pile pour les positions de la tortue
# on empile une nouvelle position au sommet de la pile à l'aide de la fonction empile.
# lorsqu'on empile, on met simplement en mémoire la position et l'orientation actuelle de la tortue.
# On dépile le sommet de la pile à l'aide de la fonction depile.
# Lorsqu'on dépile, la tortue se place dans la position et l'orientation dépilée.
pile = []
def empile() :
# on empile la position actuelle de la tortue :
pile.append(position())
# on empile l'orientation actuelle de la tortue :
pile.append(heading())
def depile() :
# on lève le crayon afin que la tortue ne trace pas
# le déplacement provoqué.
penup()
# la tortue prend l'orientation enregistrée en tête de pile
# et on efface cette tête de pile :
setheading(pile.pop())
# la tortue rejoint la position enregistrée en tête de pile
# et on efface cette tête de pile :
setposition(pile.pop())
# on réabaisse le crayon puisque la tortue va reprendre le tracé
# à partir de la position que l'on vient de rejoindre.
pendown()
def regle(chaineInitiale, nbtransfo) :
"""
Règle de substitution : F devient F[+F]F[-F]F
"""
for _ in range(nbtransfo) :
chaineInitiale = chaineInitiale.replace('F','F[+F]F[-F]F')
return chaineInitiale
def dessine(ch, unite, angle) :
""" interprétation de la chaîne par la tortue."""
# parcours de la chaine de caractères :
for x in ch :
# interprétation du caractère lu :
if x == 'F' :
forward(unite)
elif x == '+' :
left(angle)
elif x == '-' :
right(angle)
elif x == '[' :
empile()
elif x == ']' :
depile()
# mise à jour de la fenêtre de tracé :
definitFenetre()
def miseAjourExtremeTortue() :
"""
Met à jour les valeurs min et max des abscisses
et ordonnées prises par la tortue lors de ses pérégrinations.
"""
# min des x de la tortue
# (le min des positions précédentes est enregistré dans tortueExtreme[0],
# on prend le min des positions précédentes et de la position actuelle)
tortueExtreme[0] = min( tortueExtreme[0], position()[0])
# max des x de la tortue :
tortueExtreme[2] = max( tortueExtreme[2], position()[0])
# min des y de la tortue :
tortueExtreme[1] = min( tortueExtreme[1], position()[1])
# max des y de la tortue :
tortueExtreme[3] = max( tortueExtreme[3], position()[1])
def definitFenetre() :
"""
On définit une fenêtre carré de tracé en définissant
son coin inférieur gauche (xmin, ymin)
et son coin supérieur droit (xmax, ymax).
La définition des deux coins du coin est obtenue à l'aide du centre
défini lui-même à partir des positions extrêmes qui ont été prises par la tortue
lors de l'ensemble de ses déplacements.
(La fenêtre est définie carrée plutôt que rectangulaire afin d'éviter
un effet d'écrasement sur une direction.)
"""
miseAjourExtremeTortue()
# coordonnées du centre de la nouvelle fenêtre :
xc = (tortueExtreme[0] + tortueExtreme[2]) * 0.5
yc = (tortueExtreme[1] + tortueExtreme[3]) * 0.5
# delta=max(hauteur, largeur) de la nouvelle fenêtre
# pour définir largeur=hauteur pour la nouvelle fenêtre :
delta = max( tortueExtreme[2] - tortueExtreme[0], tortueExtreme[3] - tortueExtreme[1])
# calcul des coins inférieurs gauche
# et supérieur droit de la nouvelle fenêtre :
delta = delta * 0.5
xmin, ymin = xc -delta, yc -delta
xmax, ymax = xc + delta, yc + delta
# ouverture de la fenêtre sur ces nouveaux paramètres :
setworldcoordinates(xmin, ymin, xmax, ymax)
# liste enregistrant les xmin, ymin, xmax, ymax prises par
# la tortue au cours de ses pérégrinations.
# Cette liste est mise à jour par la fonction miseAjourExtremeTortue()
# après chaque déplacement de la tortue :
tortueExtreme = [ 0, 0, 1, 1]
# fenêtre graphique pour le tracé
# caractérisée par le coin inférieur gauche (xmin, ymin)
# et le coin supérieur droit (xmax, ymax).
# Cette fenêtre est redéfinie après chaque déplacement de la tortue
# à l'aide de la fonction definitFenetre().
definitFenetre()
speed(0) # tortue rapide
pencolor('green') # tracé en vert
setheading(90) # la tortue commence orientée vers le haut
dessine( regle(chaineInitiale = 'F', nbtransfo = 5), unite = 1, angle = 30 )
hideturtle() # on masque la tortue
mainloop() # maintenir fenêtre ouverte
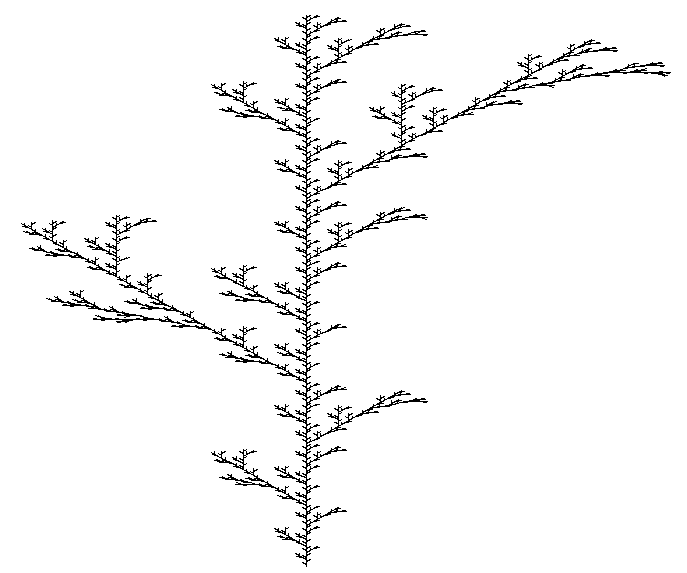
Une plante L system (2).
On reprend le principe expliqué dans l' exercice précédent.
La règle de substitution est maintenant : chaque lettre F est remplacée par F-[-F+F+F]+[+F-F-F]F.
On interprète maintenant une chaîne de caractères, en parcourant ses caractères dans l'ordre,
à l'aide d'une tortue de la façon suivante :
- à chaque lettre F, la tortue avance d'une unité (dans la direction donnée par sa tête),
- à chaque signe + rencontré, la tortue tourne sur la gauche de 20 degrés,
- à chaque signe - rencontré, la tortue tourne sur la droite de 20 degrés.
- à chaque symbole [ rencontré, la position (coordonnées+orientation de la tête) de la tortue est empilée.
- à chaque symbole ] rencontré, la position de la tortue est dépilée.
On part de la chaîne ch='F', on transforme cette chaîne un certain nombre de fois suivant le processus
de transformation exposé. Puis on interprète la chaîne finale suivant le principe précédent.
Programmez...
On modifie simplement quelques paramètres dans le programme de l'exercice précédent.
from turtle import *
# liste servant de pile pour les positions de la tortue
# on empile une nouvelle position au sommet de la pile à l'aide de la fonction empile.
# lorsqu'on empile, on met simplement en mémoire la position et l'orientation actuelle de la tortue.
# On dépile le sommet de la pile à l'aide de la fonction depile.
# Lorsqu'on dépile, la tortue se place dans la position et l'orientation dépilée.
pile = []
def empile() :
# on empile la position actuelle de la tortue :
pile.append(position())
# on empile l'orientation actuelle de la tortue :
pile.append(heading())
def depile() :
# on lève le crayon afin que la tortue ne trace pas
# le déplacement provoqué.
penup()
# la tortue prend l'orientation enregistrée en tête de pile
# et on efface cette tête de pile :
setheading(pile.pop())
# la tortue rejoint la position enregistrée en tête de pile
# et on efface cette tête de pile :
setposition(pile.pop())
# on réabaisse le crayon puisque la tortue va reprendre le tracé
# à partir de la position que l'on vient de rejoindre.
pendown()
def regle(chaineInitiale, nbtransfo) :
"""
Règle de substitution : F devient F-[-F+F+F]+[+F-F-F]F
"""
for _ in range(nbtransfo) :
chaineInitiale = chaineInitiale.replace('F','F-[-F+F+F]+[+F-F-F]F')
return chaineInitiale
def dessine(ch, unite, angle) :
""" interprétation de la chaîne par la tortue."""
# parcours de la chaine de caractères :
for x in ch :
# interprétation du caractère lu :
if x == 'F' :
forward(unite)
elif x == '+' :
left(angle)
elif x == '-' :
right(angle)
elif x == '[' :
empile()
elif x == ']' :
depile()
# mise à jour de la fenêtre de tracé :
definitFenetre()
def miseAjourExtremeTortue() :
"""
Met à jour les valeurs min et max des abscisses
et ordonnées prises par la tortue lors de ses pérégrinations.
"""
# min des x de la tortue
# (le min des positions précédentes est enregistré dans tortueExtreme[0],
# on prend le min des positions précédentes et de la position actuelle)
tortueExtreme[0] = min( tortueExtreme[0], position()[0])
# max des x de la tortue :
tortueExtreme[2] = max( tortueExtreme[2], position()[0])
# min des y de la tortue :
tortueExtreme[1] = min( tortueExtreme[1], position()[1])
# max des y de la tortue :
tortueExtreme[3] = max( tortueExtreme[3], position()[1])
def definitFenetre() :
"""
On définit une fenêtre carré de tracé en définissant
son coin inférieur gauche (xmin, ymin)
et son coin supérieur droit (xmax, ymax).
La définition des deux coins du coin est obtenue à l'aide du centre
défini lui-même à partir des positions extrêmes qui ont été prises par la tortue
lors de l'ensemble de ses déplacements.
(La fenêtre est définie carrée plutôt que rectangulaire afin d'éviter
un effet d'écrasement sur une direction.)
"""
miseAjourExtremeTortue()
# coordonnées du centre de la nouvelle fenêtre :
xc = (tortueExtreme[0] + tortueExtreme[2]) * 0.5
yc = (tortueExtreme[1] + tortueExtreme[3]) * 0.5
# delta=max(hauteur, largeur) de la nouvelle fenêtre
# pour définir largeur=hauteur pour la nouvelle fenêtre :
delta = max( tortueExtreme[2] - tortueExtreme[0], tortueExtreme[3] - tortueExtreme[1])
# calcul des coins inférieurs gauche
# et supérieur droit de la nouvelle fenêtre :
delta = delta * 0.5
xmin, ymin = xc -delta, yc -delta
xmax, ymax = xc + delta, yc + delta
# ouverture de la fenêtre sur ces nouveaux paramètres :
setworldcoordinates(xmin, ymin, xmax, ymax)
# liste enregistrant les xmin, ymin, xmax, ymax prises par
# la tortue au cours de ses pérégrinations.
# Cette liste est mise à jour par la fonction miseAjourExtremeTortue()
# après chaque déplacement de la tortue :
tortueExtreme = [ 0, 0, 1, 1]
# fenêtre graphique pour le tracé
# caractérisée par le coin inférieur gauche (xmin, ymin)
# et le coin supérieur droit (xmax, ymax).
# Cette fenêtre est redéfinie après chaque déplacement de la tortue
# à l'aide de la fonction definitFenetre().
definitFenetre()
speed(0) # tortue rapide
pencolor('green') # tracé en vert
setheading(90) # la tortue commence orientée vers le haut
dessine( regle(chaineInitiale = 'F', nbtransfo = 5), unite = 1, angle = 20 )
hideturtle() # on masque la tortue
mainloop() # maintenir fenêtre ouverte






