Tourne à gauche.
Sur la figure ci-dessous, un personnage se déplace le long du segment [AB] de A vers B puis se dirige vers l'un des points G verts (dans ce cas, il tourne à gauche) ou vers l'un des points D oranges (dans ce cas, il tourne à droite).
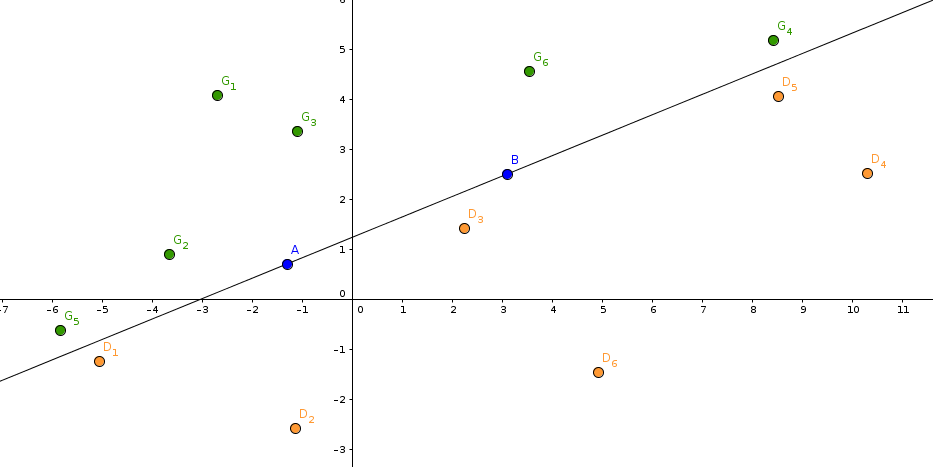
Les points sont donnés par leurs coordonnées.
Écrire une fonction python tourneGauche spécifiée ainsi :
- Entrées : A, B et un point C ne se trouvant pas sur la droite (AB).
- Sortie : True si un personnage allant de A en B puis de B en C tourne à gauche en B, False sinon.
Écrire ensuite la fonction tourneDroite analogue.
Pour distinguer le fait de tourner à droite ou à gauche,
on peut par exemple raisonner sur l'angle de vecteurs
\( \left( \overrightarrow{AB}, \overrightarrow{AC} \right) \)
(ou \( \left( \overrightarrow{AB}, \overrightarrow{BC} \right) \)
si vous préférez, il vous faudra alors adapter ce qui suit).
En faisant le choix proposé,
on voit que les mesures principales
des angles \( \left( \overrightarrow{AB}, \overrightarrow{AG} \right) \)
sont dans l'intervalle \( \left] 0 ; \pi \right[ \)
donc à sinus strictement positif (ou encore à déterminant strictement positif).
Tandis que les mesures principales des angles
\( \left( \overrightarrow{AB}, \overrightarrow{AD} \right) \)
sont dans l'intervalle \( \left] -\pi ; 0 \right[ \)
donc à sinus strictement négatif (ou encore à déterminant strictement négatif).
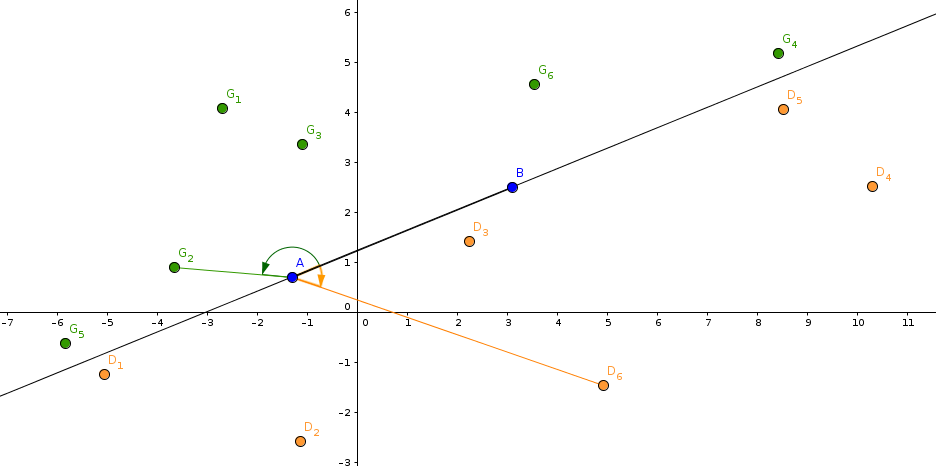
D'où la proposition suivante :
"""
Un repère du plan est fixé.
Les coordonnées des points sont données dans ce repère.
Un point est donné par le tuple de ses deux coordonnées.
"""
def vecteur(A,B):
""" A=(A[0],A[1]) et B=(B[0],B[1]) deux points.
la fonction retourne le tuple des coordonnées du vecteur u=vec(AB),
c'est à dire (B[0]-A[0], B[1]-A[1])."""
return (B[0]-A[0], B[1]-A[1])
def determinant(u,v):
"""déterminant des vecteurs u=(u[0],u[1]) et v=(v[0],v[1])."""
return u[0]*v[1]-u[1]*v[0]
def alignes(A,B,C) :
"""Un triplet A, B, C, on retourne True si A, B, C alignés,
retourne False sinon."""
return determinant(vecteur(A,B),vecteur(A,C)) == 0
def tourneGauche(A, B, C) :
""" A, B, C trois points d'un plan donnés par leurs coordonnées.
Un personnage parcourt le segment [AB] de A vers B puis le segment [BC]
de B vers C.
La fonction retourne True si en B le personnage tourne vers sa gauche,
et retourne False sinon.
"""
return determinant(vecteur(A,B),vecteur(A,C)) > 0
def tourneDroite(A, B, C) :
""" A, B, C trois points d'un plan donnés par leurs coordonnées.
Un personnage parcourt le segment [AB] de A vers B puis le segment [BC]
de B vers C.
La fonction retourne True si en B le personnage tourne vers sa droite,
et retourne False sinon.
"""
return determinant(vecteur(A,B),vecteur(A,C)) < 0
A = (1,1)
B = (3,3)
C = (5,5)
print("Cas d'un point C aligné avec A et B : ")
print("Parcours A(1;1) -> B(3;3) -> C(5;5). Tourne à gauche ? ", tourneGauche(A, B, C) )
print("Parcours A(1;1) -> B(3;3) -> C(5;5). Tourne à droite ? ", tourneDroite(A, B, C) )
print()
C = (-2, 6)
print("Cas d'un point C du même côté de la droite (AB) que les points G : ")
print("Parcours A(1;1) -> B(3;3) -> C(-2;6). Tourne à gauche ? ", tourneGauche(A, B, C) )
print("Parcours A(1;1) -> B(3;3) -> C(-2;6). Tourne à droite ? ", tourneDroite(A, B, C) )
print()
C = (10, -4)
print("Cas d'un point C du même côté de la droite (AB) que les points D : ")
print("Parcours A(1;1) -> B(3;3) -> C(10;-4). Tourne à gauche ? ", tourneGauche(A, B, C) )
print("Parcours A(1;1) -> B(3;3) -> C(10;-4). Tourne à droite ? ", tourneDroite(A, B, C) )
print()
Affichage :
Cas d'un point C aligné avec A et B :
Parcours A(1;1) -> B(3;3) -> C(5;5). Tourne à gauche ? False
Parcours A(1;1) -> B(3;3) -> C(5;5). Tourne à droite ? False
Cas d'un point C du même côté de la droite (AB) que les points G :
Parcours A(1;1) -> B(3;3) -> C(-2;6). Tourne à gauche ? True
Parcours A(1;1) -> B(3;3) -> C(-2;6). Tourne à droite ? False
Cas d'un point C du même côté de la droite (AB) que les points D :
Parcours A(1;1) -> B(3;3) -> C(10;-4). Tourne à gauche ? False
Parcours A(1;1) -> B(3;3) -> C(10;-4). Tourne à droite ? True
En avant.
Avec le programme proposé dans l'exercice précédent, on ne peut pas distinguer les deux cas d'alignement : cas où les vecteurs \( \overrightarrow{AB} \) et \( \overrightarrow{BC} \) sont dans le même sens, et cas où ils sont en sens opposés (le personnage fait un demi-tour).
De façon plus générale, traçons la perpendiculaire à (AB) passant par B. On peut estimer, si le point C est du même côté de la perpendiculaire que le point A, que le personnage fait marche arrière (au moins partiellement). Tandis que notre personnage fait marche avant si le point C et le point A ne sont pas du même côté de la perpendiculaire.
On découpe ainsi le plan en quatre zones principales, auxquelles il faut ajouter les 4 demi-droites d'origine B :
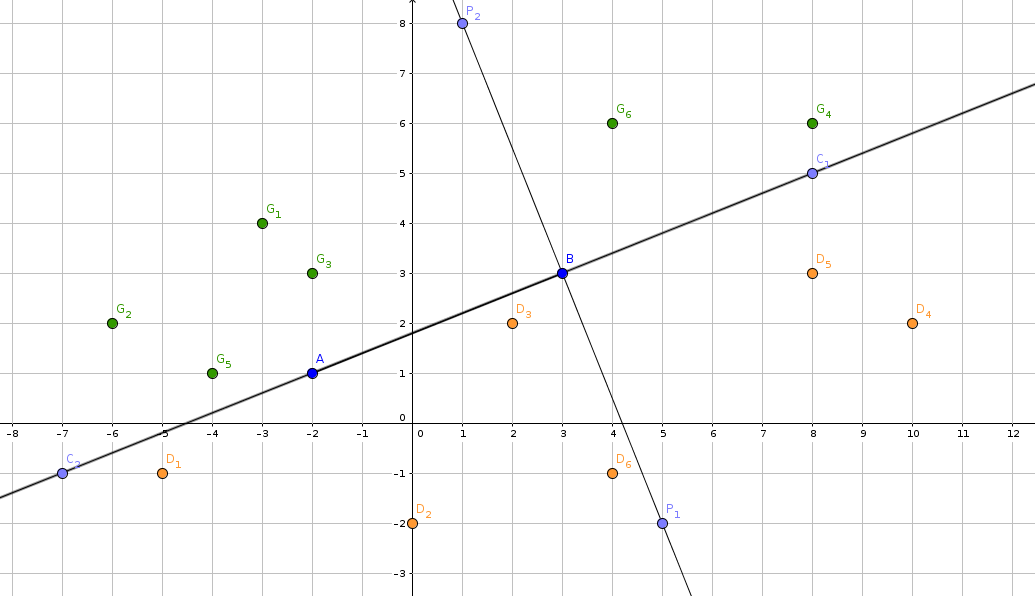
Votre mission est maintenant de compléter
le programme précédent par une fonction situant
notre personnage dans l'une de ses zones (au total 8 zones).
La fonction présentera en entrée les points A, B, C et
donnera en sortie des messages tels que "tourne à gauche, vers l'avant",
ou "tourne à gauche à angle droit" ou encore "tourne à droite vers l'arrière" ou encore "fait demi-tour" …
C'est maintenant le cosinus (et donc le produit scalaire) qui va nous permettre de compléter.
Pour les points du même côté
que A de la perpendiculaire,
l'angle de vecteurs \( \left( \overrightarrow{AB} , \overrightarrow{BC} \right) \)
a une mesure principale
hors de l'intervalle \( \left[ \frac{-\pi}{2} ; \frac{\pi}{2} \right] \),
le cosinus et le produit scalaire sont donc strictement négatifs.
Pour les points de l'autre côté de la perpendiculaire,
le produit scalaire est strictement positif. Il est nul sur la perpendiculaire.
D'où le programme :
"""
Un repère du plan est fixé.
Les coordonnées des points sont données dans ce repère.
Un point est donné par le tuple de ses deux coordonnées.
"""
def vecteur(A,B):
""" A=(A[0],A[1]) et B=(B[0],B[1]) deux points.
la fonction retourne le tuple des coordonnées du vecteur u=vec(AB),
c'est à dire (B[0]-A[0], B[1]-A[1])."""
return (B[0]-A[0], B[1]-A[1])
def determinant(u,v):
"""retourne le déterminant des vecteurs u=(u[0],u[1]) et v=(v[0],v[1])."""
return u[0]*v[1]-u[1]*v[0]
def produitscalaire(u,v) :
"""retourne le produit scalaire des vecteurs
u=(u[0],u[1]) et v=(v[0],v[1])."""
return u[0]*v[0] + u[1]*v[1]
def alignes(A,B,C) :
"""Un triplet A, B, C, on retourne True si A, B, C alignés,
retourne False sinon."""
return determinant(vecteur(A,B),vecteur(A,C)) == 0
def tourneGauche(A, B, C) :
""" A, B, C trois points d'un plan donnés par leurs coordonnées.
Un personnage parcourt le segment [AB] de A vers B puis le segment [BC]
de B vers C.
La fonction retourne True si en B le personnage tourne vers sa gauche,
et retourne False sinon.
"""
return determinant(vecteur(A,B),vecteur(B,C)) > 0
def tourneDroite(A, B, C) :
""" A, B, C trois points d'un plan donnés par leurs coordonnées.
Un personnage parcourt le segment [AB] de A vers B puis le segment [BC]
de B vers C.
La fonction retourne True si en B le personnage tourne vers sa droite,
et retourne False sinon.
"""
return determinant(vecteur(A,B),vecteur(B,C)) < 0
def enAvant(A, B, C) :
""" retourne True si C est en avant après le parcours A -> B
et retourne False sinon."""
return produitscalaire(vecteur(A,B),vecteur(B,C)) > 0
def enArriere(A, B, C) :
""" retourne True si C est en arrière après le parcours A -> B
et retourne False sinon."""
return produitscalaire(vecteur(A,B),vecteur(B,C)) < 0
def quartDeTour(A, B, C) :
""" retourne True si C est à angle droit après le parcours A -> B
et retourne False sinon."""
return produitscalaire(vecteur(A,B),vecteur(B,C)) == 0
def zone(A, B, C) :
d = determinant(vecteur(A,B),vecteur(B,C))
p = produitscalaire(vecteur(A,B),vecteur(B,C))
if d > 0 :
if p > 0 :
return " en avant, gauche."
elif p < 0 :
return " en arrière, gauche."
else : # cas p == 0
return "à angle droit, gauche."
elif d < 0 :
if p > 0 :
return " en avant, droite."
elif p < 0 :
return " en arrière, droite."
else : # cas p == 0
return "à angle droit, droite."
else : # cas d == 0
if p > 0 :
return " en avant, tout droit."
elif p < 0 :
return " demi-tour."
else : # cas p == 0
return "J'y suis, j'y reste."
# les points sont ceux du graphique de l'énoncé
A = (-2,1)
B = (3,3)
G6 = (4, 6) # en avant gauche
D5 = (8,3) # en avant droite
P1 = (5, -2) # à angle droit, droite
P2 = (1,8) # à angle droit, gauche
C1 = (8, 5) # alignement, en avant
C2 = (-7,-1) # alignement, en arrière
G3 = (-2, 3) # en arrière, gauche
D2 = (0, -2) # en arrière, droite
L = ( G6, D5, P1, P2, C1, C2, G3, D2, B)
for M in L :
print("Point {} : ".format(M),zone(A, B, M))
Affichage :
Point (4, 6) : en avant, gauche.
Point (8, 3) : en avant, droite.
Point (5, -2) : à angle droit, droite.
Point (1, 8) : à angle droit, gauche.
Point (8, 5) : en avant, tout droit.
Point (-7, -1) : demi-tour.
Point (-2, 3) : en arrière, gauche.
Point (0, -2) : en arrière, droite.
Point (3, 3) : J'y suis, j'y reste.


