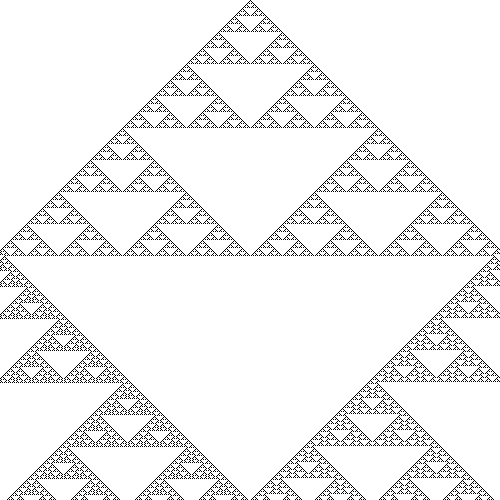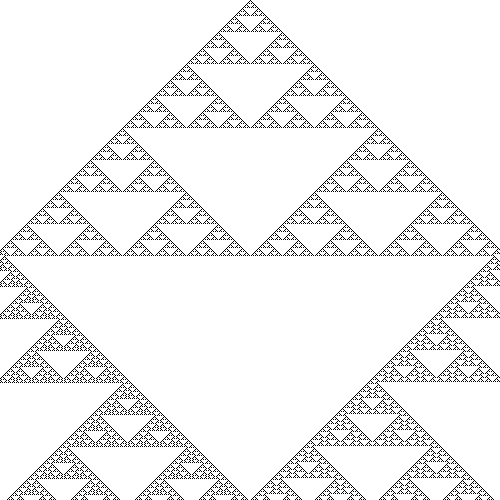Dans ces exercices d'application, nous n'écrirons dans les fichiers que des '0' et des '1'.
Nous allons en effet travailler sur des fichiers d'images monochromes (au format pbm présenté dans l'exercice 1).
Règle 30.
Dans un fichier au format pbm, la première ligne est constituée de pixels blancs, sauf le pixel central qui est noir.
On détermine les couleurs des pixels de la ligne suivante ainsi :
- Si un pixel noir a son voisin gauche noir et son voisin droit noir, alors il devient blanc à la ligne suivante.
- Si un pixel noir a son voisin gauche noir et son voisin droit blanc, alors il devient blanc à la ligne suivante.
- Si un pixel blanc a son voisin gauche noir et son voisin droit noir, alors il reste blanc à la ligne suivante.
- Si un pixel blanc a son voisin gauche noir et son voisin droit blanc, alors il devient noir à la ligne suivante.
- Si un pixel noir a son voisin gauche blanc et son voisin droit noir, alors il reste noir à la ligne suivante.
- Si un pixel noir a son voisin gauche blanc et son voisin droit blanc, alors il devient noir à la ligne suivante.
- Si un pixel blanc a son voisin gauche blanc et son voisin droit noir, alors il devient noir à la ligne suivante.
- Si un pixel blanc a son voisin gauche blanc et son voisin droit blanc, alors il reste blanc à la ligne suivante.
En associant 0 à blanc et 1 à noir, les règles de transformation sont les suivantes (les entiers à 3 bits de la ligne 1 sont
rangés en ordre décroissant) :
Règle 30
| 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
Le nombre 00011110 en binaire s'écrivant 30 en décimal, vous avez l'explication du nom donné à cette règle.
On détermine les couleurs des pixels de la ligne 2 à partir de la ligne 1 en appliquant la règle 30, puis
les couleurs des pixels de la ligne 3 à partir de la ligne 2 avec la règle 30, et ainsi de suite...
Programmez !
- Le nombre total de lignes à calculer sera demandé à l'utilisateur en début de programme.
On décide ici que l'image sera carrée.
- on décide ici qu'un pixel (ou cellule dans le vocabulaire des automates cellulaires) en bordure gauche de la feuille a un voisin
gauche blanc. Idem pour le voisin droit d'une cellule du bord droit.
Remarque : dans le fichier texte, aucune ligne (dans le format pbm) ne doit dépasser 70 caractères.
On est donc allé à la ligne à chaque nouveau caractère (une ligne de l'image correspond à la lecture
de largeur caractères '0'
ou '1' qui se succèdent, il n'est pas besoin que les caractères soient eux-mêmes sur la même ligne.)
nb=int(input('Entrez le nombre de lignes : '))
largeur=nb
hauteur=largeur
# t : liste de lignes
# t[0] : ligne 1, longueur nb+2 (on ajoute un blanc à gauche et un à droite)
# les cellules visibles de t[0] seront donc t[0][1], t[0][2], ..., t[0][nb].
# dernière ligne : t[nb-1]
t=[['0' for j in range(nb+2)] for k in range(nb)]
# on place un '1', c'est à dire un noir au centre de la première ligne
t[0][(nb+2)//2]='1'
# dictionnaire des transformations :
regle={'111' : '0', '110' : '0', '101' : '0',\
'100' : '1', '011' : '1', '010' : '1', '001' : '1', '000' : '0'}
for k in range(1,nb) :
# détermination de la ligne suivante et mise à jour de t :
for j in range(1,nb+1):
t[k][j]=regle[t[k-1][j-1]+t[k-1][j]+t[k-1][j+1]]
#ouverture du fichier en écriture :
f=open('regle30','w') # sous windows, nommer avec l'extension : regle30.pbm
# déclaration de l'entête pour fichier pbm texte :
f.write('P1\n')
f.write(str(largeur)+' '+str(hauteur)+'\n')
for l in range(nb) :
for c in range(1,nb+1) :
f.write(t[l][c])
f.write('\n')
# fermeture du fichier
f.close()

Règle 90.
Dans un fichier au format pbm, la première ligne est constituée de pixels blancs, sauf le pixel central qui est noir.
On détermine les couleurs des pixels de la ligne 2 à partir de la ligne 1 en appliquant la règle 90, puis
les couleurs des pixels de la ligne 3 à partir de la ligne 2 avec la règle 90, et ainsi de suite.
- Explicitez ce qu'est la règle 90 en reprenant l'énoncé de l'exercice précédent.
- Programmez.
Tableau de la règle 90.
Règle 90
| 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Il suffit de modifier le dictionnaire dans le programme précédent.
nb=int(input('Entrez le nombre de lignes : '))
largeur=nb
hauteur=largeur
t=[['0' for j in range(nb+2)] for k in range(nb)]
t[0][(nb+2)//2]='1'
# dictionnaire des transformations :
regle={'111' : '0', '110' : '1', '101' : '0',\
'100' : '1', '011' : '1', '010' : '0', '001' : '1', '000' : '0'}
# calcul du tableau des lignes :
for k in range(1,nb) :
for j in range(1,nb+1):
t[k][j]=regle[t[k-1][j-1]+t[k-1][j]+t[k-1][j+1]]
# fabrication de l'image pbm :
f=open('regle90','w') # sous windows, nommer avec l'extension : regle90.pbm
f.write('P1\n')
f.write(str(largeur)+' '+str(hauteur)+'\n')
for l in range(nb) :
for c in range(1,nb+1) :
f.write(t[l][c])
f.write('\n')
f.close()