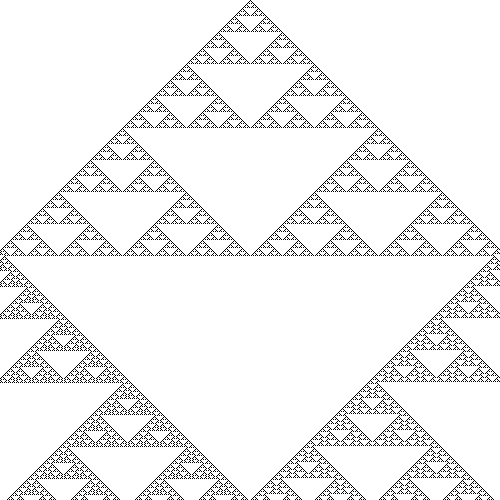Dans ces exercices d'application, nous n'écrirons dans les fichiers que des '0' et des '1'.
Nous allons en effet travailler sur des fichiers d'images monochromes (au format pbm présenté dans l'exercice 1).
Présentation du format pbm.
Le format pbm est un format simple d'image en noir et blanc.
Il existe en fait deux types de format pbm : le format texte (ou ascii) et le format binaire.
Dans un premier temps, nous utiliserons le format texte.
Une image est formée d'un rectangle de pixels, c'est à dire d'un rectangle de points colorés.
Une image de 10 pixels sur 10 pixels au format pbm est tout simplement un fichier contenant 10 lignes, chacune de ces lignes
est constituée de 0 et de 1. Chaque 0 est interprété dans ce format par un pixel blanc et chaque 1 par un pixel noir.
Nous voulons par exemple créer une image de 10 pixels sur 10 pixels formée d'une alternance de lignes blanches et lignes noires,
:
 (le cadre rouge ne fait pas partie de l'image, il sert ici simplement
à la mettre en évidence.)
(le cadre rouge ne fait pas partie de l'image, il sert ici simplement
à la mettre en évidence.)
Pour cela, il suffit d'inscrire le code suivant dans un fichier à l'aide d'un éditeur de texte :
P1
10 10
0000000000
0000000000
1111111111
1111111111
0000000000
0000000000
1111111111
1111111111
0000000000
0000000000
La première ligne P1 permet de reconnaître le format pbm texte, la ligne suivante (10 10) est constituée de la
largeur, suivie de la hauteur (en pixels) de l'image.
Les lignes suivantes définissent les couleurs (blanc ou noir) des pixels de l'image.
- Copier, coller le texte précédent dans un fichier ouvert avec un simple éditeur de texte.
Nommer le fichier bidule.pbm et visualiser l'image avec un logiciel adéquat (gimp par exemple)
(sous linux, l'extension pbm est inutile).
- Créer maintenant un tel fichier à l'aide d'un programme python. La largeur et la hauteur du fichier image
devront être demandées à l'utilisateur, ainsi que l'épaisseur d'une ligne (remarque pour simplifier
l'écriture : on peut ajouter des lignes de 1 et 0 dans
le fichier texte au-delà de la ligne de numéro hauteur, ces lignes ne seront pas prises en compte.)
Une solution possible est présentée ci-dessous. Prenez le temps de tester, de faire des modifications, d'ouvrir les fichiers
images associés...
largeur=int(input('Entrez la largeur de l\'image en pixels : '))
hauteur=int(input('Entrez la hauteur de l\'image en pixels : '))
nom=input('Entrez le nom du fichier : ')
epais=int(input("Entrez l'épaisseur d'une ligne (en pixels) : "))
#ouverture du fichier en écriture :
f=open(nom,'w') # sous windows, écrire plutôt f=open(nom+'.pbm','w')
# déclaration de l'entête pour fichier pbm texte :
f.write('P1\n')
f.write(str(largeur)+' '+str(hauteur)+'\n')
def ligneEpaisseurUn(couleur) :
for j in range(largeur) :
f.write(couleur)
f.write('\n')
def ligne(couleur) :
for j in range(epais) :
ligneEpaisseurUn(couleur)
nbLignes=0
while nbLignes <= hauteur :
ligne('0')
ligne('1')
nbLignes+=(2*epais)
f.close()
Carrés emboîtés.
L'objectif dans cet exercice est de produire des images de carrés emboîtés comme suit (le cadre rouge ne fait
pas partie de l'image, il n'est là que pour la délimiter) :


L'image est constituée de n carrés blancs 'emboîtés' (n est demandé à l'utilisateur) de largeur 1 pixel,
deux carrés blancs sont séparés par un carré noir (de largeur 1 pixel également). Le plus grand carré est blanc, il a les
dimensions de l'image. Le plus petit carré, au centre, est noir : il est constitué d'un seul pixel.
Programmez !
Dans la solution proposée ici, on a utilisé une liste de listes.
Si par exemple, t=[[2,8,9],[4,5,7]], t est une liste constituée des deux listes t[0]=[2,8,9] et t[1]=[4,5,7].
Le nombre 8 est par exemple t[0][1].
Tous les calculs nécessaires sont effectués à l'aide de la liste de listes. Ce n'est qu'ensuite que l'on ouvre un fichier
et que l'on écrit les 0 et les 1 dans le fichier.
nb=int(input('Entrez le nombre de carrés noirs : '))
largeur=3+4*(nb-1) # côté du plus grand carré
hauteur=largeur
# définition d'une liste de listes
# correspondant au rectangle de pixels
# tout à 1 = tous les pixels noirs au départ
t=[]
for k in range(largeur) :
t.append(['1']*largeur)
# boucle coloriant le plus gd carré en blanc
# puis le carré de taille juste en dessous
# puis ...
# finit par le plus petit carré blanc, de côté 3
cote=largeur
for c in range(1,nb+1) : # c: numéro du carré
a=2*(c-1) # (a,a) coordonnées coin sup gauche du carré
# blanc à tracer
# boucle pour les pixels du carré blanc :
for k in range(a,a+cote) :
t[a][k]='0'
t[a+cote-1][k]='0'
t[k][a]='0'
t[k][a+cote-1]='0'
cote-=4
#ouverture du fichier en écriture :
f=open('carresemboites','w') # sous windows, nommer avec l'extension : carresemboites.pbm
# déclaration de l'entête pour fichier pbm texte :
f.write('P1\n')
f.write(str(largeur)+' '+str(hauteur)+'\n')
for l in range(largeur) :
for c in range(hauteur) :
f.write(t[l][c])
f.write('\n')
# fermeture du fichier
f.close()
Règle 30.
Dans un fichier au format pbm, la première ligne est constituée de pixels blancs, sauf le pixel central qui est noir.
On détermine les couleurs des pixels de la ligne suivante ainsi :
- Si un pixel noir a son voisin gauche noir et son voisin droit noir, alors il devient blanc à la ligne suivante.
- Si un pixel noir a son voisin gauche noir et son voisin droit blanc, alors il devient blanc à la ligne suivante.
- Si un pixel blanc a son voisin gauche noir et son voisin droit noir, alors il reste blanc à la ligne suivante.
- Si un pixel blanc a son voisin gauche noir et son voisin droit blanc, alors il devient noir à la ligne suivante.
- Si un pixel noir a son voisin gauche blanc et son voisin droit noir, alors il reste noir à la ligne suivante.
- Si un pixel noir a son voisin gauche blanc et son voisin droit blanc, alors il devient noir à la ligne suivante.
- Si un pixel blanc a son voisin gauche blanc et son voisin droit noir, alors il devient noir à la ligne suivante.
- Si un pixel blanc a son voisin gauche blanc et son voisin droit blanc, alors il reste blanc à la ligne suivante.
En associant 0 à blanc et 1 à noir, les règles de transformation sont les suivantes (les entiers à 3 bits de la ligne 1 sont
rangés en ordre décroissant) :
Règle 30
| 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
Le nombre 00011110 en binaire s'écrivant 30 en décimal, vous avez l'explication du nom donné à cette règle.
On détermine les couleurs des pixels de la ligne 2 à partir de la ligne 1 en appliquant la règle 30, puis
les couleurs des pixels de la ligne 3 à partir de la ligne 2 avec la règle 30, et ainsi de suite...
Programmez !
- Le nombre total de lignes à calculer sera demandé à l'utilisateur en début de programme.
On décide ici que l'image sera carrée.
- on décide ici qu'un pixel (ou cellule dans le vocabulaire des automates cellulaires) en bordure gauche de la feuille a un voisin
gauche blanc. Idem pour le voisin droit d'une cellule du bord droit.
Remarque : dans le fichier texte, aucune ligne (dans le format pbm) ne doit dépasser 70 caractères.
On est donc allé à la ligne à chaque nouveau caractère (une ligne de l'image correspond à la lecture
de largeur caractères '0'
ou '1' qui se succèdent, il n'est pas besoin que les caractères soient eux-mêmes sur la même ligne.)
nb=int(input('Entrez le nombre de lignes : '))
largeur=nb
hauteur=largeur
# t : liste de lignes
# t[0] : ligne 1, longueur nb+2 (on ajoute un blanc à gauche et un à droite)
# les cellules visibles de t[0] seront donc t[0][1], t[0][2], ..., t[0][nb].
# dernière ligne : t[nb-1]
t=[['0' for j in range(nb+2)] for k in range(nb)]
# on place un '1', c'est à dire un noir au centre de la première ligne
t[0][(nb+2)//2]='1'
# dictionnaire des transformations :
regle={'111' : '0', '110' : '0', '101' : '0',\
'100' : '1', '011' : '1', '010' : '1', '001' : '1', '000' : '0'}
for k in range(1,nb) :
# détermination de la ligne suivante et mise à jour de t :
for j in range(1,nb+1):
t[k][j]=regle[t[k-1][j-1]+t[k-1][j]+t[k-1][j+1]]
#ouverture du fichier en écriture :
f=open('regle30','w') # sous windows, nommer avec l'extension : regle30.pbm
# déclaration de l'entête pour fichier pbm texte :
f.write('P1\n')
f.write(str(largeur)+' '+str(hauteur)+'\n')
for l in range(nb) :
for c in range(1,nb+1) :
f.write(t[l][c])
f.write('\n')
# fermeture du fichier
f.close()

Règle 90.
Dans un fichier au format pbm, la première ligne est constituée de pixels blancs, sauf le pixel central qui est noir.
On détermine les couleurs des pixels de la ligne 2 à partir de la ligne 1 en appliquant la règle 90, puis
les couleurs des pixels de la ligne 3 à partir de la ligne 2 avec la règle 90, et ainsi de suite.
- Explicitez ce qu'est la règle 90 en reprenant l'énoncé de l'exercice précédent.
- Programmez.
Tableau de la règle 90.
Règle 90
| 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Il suffit de modifier le dictionnaire dans le programme précédent.
nb=int(input('Entrez le nombre de lignes : '))
largeur=nb
hauteur=largeur
t=[['0' for j in range(nb+2)] for k in range(nb)]
t[0][(nb+2)//2]='1'
# dictionnaire des transformations :
regle={'111' : '0', '110' : '1', '101' : '0',\
'100' : '1', '011' : '1', '010' : '0', '001' : '1', '000' : '0'}
# calcul du tableau des lignes :
for k in range(1,nb) :
for j in range(1,nb+1):
t[k][j]=regle[t[k-1][j-1]+t[k-1][j]+t[k-1][j+1]]
# fabrication de l'image pbm :
f=open('regle90','w') # sous windows, nommer avec l'extension : regle90.pbm
f.write('P1\n')
f.write(str(largeur)+' '+str(hauteur)+'\n')
for l in range(nb) :
for c in range(1,nb+1) :
f.write(t[l][c])
f.write('\n')
f.close()
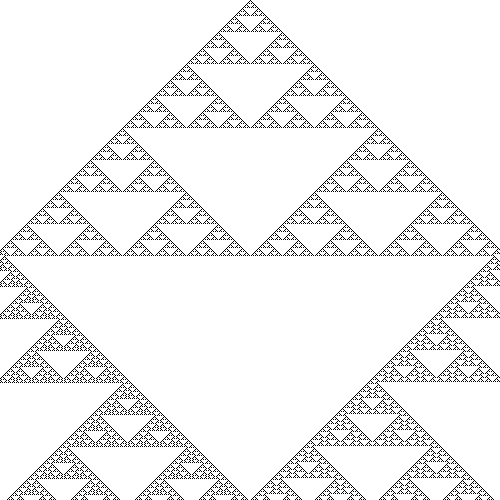
 (le cadre rouge ne fait pas partie de l'image, il sert ici simplement
à la mettre en évidence.)
(le cadre rouge ne fait pas partie de l'image, il sert ici simplement
à la mettre en évidence.)