Écriture octale d'un entier.
En langage python, on obtient l'écriture octale d'un entier avec la fonction oct.
Exemples :
def imprimeEcritOct(n) :
""" imprime l'écriture octale de l'entier n
donné en entrée en écriture décimale."""
print(" L'écriture octale python de l'entier {} est {}.".format(n, oct(n)))
print(" L'écriture octale 'mathématique' de l'entier {} est {}.".format(n, oct(n)[2:]))
print()
for j in range(16) :
imprimeEcritOct(j)
Réponse de python :
L'écriture octale python de l'entier 0 est 0o0.
L'écriture octale 'mathématique' de l'entier 0 est 0.
L'écriture octale python de l'entier 1 est 0o1.
L'écriture octale 'mathématique' de l'entier 1 est 1.
L'écriture octale python de l'entier 2 est 0o2.
L'écriture octale 'mathématique' de l'entier 2 est 2.
L'écriture octale python de l'entier 3 est 0o3.
L'écriture octale 'mathématique' de l'entier 3 est 3.
L'écriture octale python de l'entier 4 est 0o4.
L'écriture octale 'mathématique' de l'entier 4 est 4.
L'écriture octale python de l'entier 5 est 0o5.
L'écriture octale 'mathématique' de l'entier 5 est 5.
L'écriture octale python de l'entier 6 est 0o6.
L'écriture octale 'mathématique' de l'entier 6 est 6.
L'écriture octale python de l'entier 7 est 0o7.
L'écriture octale 'mathématique' de l'entier 7 est 7.
L'écriture octale python de l'entier 8 est 0o10.
L'écriture octale 'mathématique' de l'entier 8 est 10.
L'écriture octale python de l'entier 9 est 0o11.
L'écriture octale 'mathématique' de l'entier 9 est 11.
L'écriture octale python de l'entier 10 est 0o12.
L'écriture octale 'mathématique' de l'entier 10 est 12.
L'écriture octale python de l'entier 11 est 0o13.
L'écriture octale 'mathématique' de l'entier 11 est 13.
L'écriture octale python de l'entier 12 est 0o14.
L'écriture octale 'mathématique' de l'entier 12 est 14.
L'écriture octale python de l'entier 13 est 0o15.
L'écriture octale 'mathématique' de l'entier 13 est 15.
L'écriture octale python de l'entier 14 est 0o16.
L'écriture octale 'mathématique' de l'entier 14 est 16.
L'écriture octale python de l'entier 15 est 0o17.
L'écriture octale 'mathématique' de l'entier 15 est 17.
L'écriture octale d'un entier est constituée des seuls chiffres 0, 1, 2, 3, 4, 5, 6, 7.
En python, cette écriture est préfixée par '0o'.
Que signifient les chiffres d'une écriture octale ?
L'écriture décimale (ou écriture en base 10) d'un entier s'interprète par une somme de puissances de 10.
Exemple : \( 8753= 8 \times 10^3 + 7 \times 10^2 + 5 \times 10^1 +3 \times 10^0 \).
De façon générale, si le chiffre des unités (en écriture décimale) d'un entier n est b0, le chiffre des dizaines
b1, le chiffre des centaines b2 ...,
on peut écrire
n=b0 \( \times \) 100+b1\( \times \)101
+b2\( \times \)102+...
où chacun des bi est un chiffre entre 0 et 9.
L'interprétation d'une écriture octale (ou écriture en base 8) est similaire,
mais les chiffres bi sont compris entre 0 et 7 et il s'agit
de puissances de 8 au lieu des puissances de 10.
Exemple : 0o751= \( 1 \times 8^0 +5 \times 8^1 +7 \times 8^2 \).
On a donc 0o751 = 489.
Vérifions cela avec python :
print(int(0o751))
Réponse de python :
489
Notations.
Pour distinguer l'écriture en base huit d'une écriture dans une autre base, on utilisera la notation python (préfixe 0o)
ou l'on mettra huit en indice. L'absence d'indication sous-entendra une écriture en base 10.
Exemple : 0o751 = 751huit=489= 489dix.
Passer de la base 8 à la base 10.
L'exemple précédent a montré comment passer d'une écriture octale à une écriture décimale.
Exercez-vous.
Du décimal à l'octal
Un théorème.
Tout entier naturel possède une écriture octale, et une seule.
Les chiffres en décimal
Rappelons comment on obtient les chiffres, un à un, d'une écriture décimale sur un exemple.
Exemple : 8753.
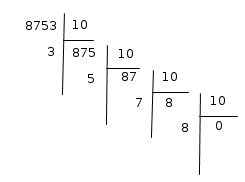
Les restes successifs sont les chiffres de l'entier. La cascade (l'algorithme) s'arrête lorsqu'on obtient un
quotient nul.
Le même algorithme dans lequel nous remplaçons 10 par 8 donne les chiffres de l'écriture octale de n.
Entrée : un entier n.
Traitement : a ← n
tant_que a est non nul :
r ← reste de la division de a par 8
a ← quotient de la division de a par 8
fin_tant_que
Sortie : les valeurs successives de r
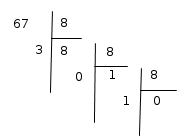
Exemple : obtenir les chiffres de l'écriture octale de 67.
a= 67 et a=8*8+3, le chiffre de rang 0 (chiffre de poids \( 8^0\) ) est donc 3.
a=8. a=8*1+0. Le bit de rang 1 (chiffre de poids \( 8^1 \) ) est 0.
a=1. a=8*0+1. Le bit de rang 2 (chiffre de poids \( 8^2 \) ) est 1.
a=0. On a terminé.
L'écriture binaire de 67 est donc 103huit.
Chiffre de poids faible, chiffre de poids fort
Dans l'écriture en base b=10 ou en base b=2 ou en base b=8, on appelle poids d'un chiffre la puissance de b
dont il est coefficient.
Exemple. \(8753=8\times 10^3+ 7\times 10^2+5\times 10^1+3\times 10^0\) : le poids de 3 est \( 10^0\),
le poids de 5 est \(10^1\), le poids de 7 est \(10^2\) et le poids de 8 est \(10^3\).
Le chiffre 3 (chiffre des unités du nombre 8753) est appelé chiffre de poids le plus faible (ou même souvent de chiffre de poids faible).
Le chiffre 8 est le chiffre de poids le plus fort (souvent appelé chiffre de poids fort).
De même dans 103huit, le 1 écrit à gauche est le chiffre de poids le plus fort (ici de poids \(8^2\) ),
et le 3 de droite est le chiffre de poids le plus faible (de poids \(8^0\) ).
On fera attention au fait que l'algorithme présenté ci-dessus donne les chiffres dans l'ordre croissant des poids (poids le plus faible en
premier, poids le plus fort en dernier) alors que l'on écrit ensuite le nombre de gauche à droite en commençant par
écrire les chiffres de poids forts.
Passer de la base 10 à la base 8.
L'exemple précédent a montré comment passer d'une écriture décimale à une écriture binaire.
Exercez-vous.
Du binaire à l'octal et vice-versa.
Du binaire à l'octal
Comme 8=23, il est possible de passer d'une écriture binaire à une écriture octale de la façon suivante :
- On regroupe les bits de l'écriture binaire par paquets de trois, en ajoutant au besoin des 0 à gauche de l'écriture.
Par exemple, N=1011deux est écrit sous la forme N= 001 011.
- On traduit chaque paquet de trois en base huit. Avec l'exemple précédent, la paquet 001deux
s'écrit 1huit
et le paquet 011deux s'écrit 3huit.
- On 'concatène' ces chiffres : on a l'écriture octale. Ici N=13huit.
De l'octal au binaire.
Si l'on dispose de l'écriture octale d'un entier N, il suffit d'écrire chacun des chiffres de l'écriture octale
en base deux (sur trois rang, donc en ajoutant éventuellement
des zéros à gauche de chaque traduction de chiffre pour obtenir des paquets de longueur 3)
pour obtenir l'écriture en base deux de l'entier N.
Exemple. N=53huit. Quelle est l'écriture de N en base 2 ?
On a 5huit=101deux et 3huit=11deux=011deux.
D'où N=101011deux.

