L'écriture hexadécimale des entiers

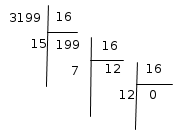
Écriture hexadécimale d'un entier.

En langage python, on obtient l'écriture hexadécimale d'un entier avec la fonction hex.

Exemples :

def imprimeEcritHex(n) :
	""" imprime l'écriture hexadécimale de l'entier n
	donné en entrée en écriture décimale."""
	print(" L'écriture hexadécimale python de l'entier {} est {}.".format(n, hex(n)))
	print(" L'écriture hexadécimale 'mathématique' de l'entier {} est {}.".format(n, hex(n)[2:]))
	print()
	
for j in range(17) :
	imprimeEcritHex(j)

Réponse de python :

 L'écriture hexadécimale python de l'entier 0 est 0x0.
 L'écriture hexadécimale 'mathématique' de l'entier 0 est 0.

 L'écriture hexadécimale python de l'entier 1 est 0x1.
 L'écriture hexadécimale 'mathématique' de l'entier 1 est 1.

 L'écriture hexadécimale python de l'entier 2 est 0x2.
 L'écriture hexadécimale 'mathématique' de l'entier 2 est 2.

 L'écriture hexadécimale python de l'entier 3 est 0x3.
 L'écriture hexadécimale 'mathématique' de l'entier 3 est 3.

 L'écriture hexadécimale python de l'entier 4 est 0x4.
 L'écriture hexadécimale 'mathématique' de l'entier 4 est 4.

 L'écriture hexadécimale python de l'entier 5 est 0x5.
 L'écriture hexadécimale 'mathématique' de l'entier 5 est 5.

 L'écriture hexadécimale python de l'entier 6 est 0x6.
 L'écriture hexadécimale 'mathématique' de l'entier 6 est 6.

 L'écriture hexadécimale python de l'entier 7 est 0x7.
 L'écriture hexadécimale 'mathématique' de l'entier 7 est 7.

 L'écriture hexadécimale python de l'entier 8 est 0x8.
 L'écriture hexadécimale 'mathématique' de l'entier 8 est 8.

 L'écriture hexadécimale python de l'entier 9 est 0x9.
 L'écriture hexadécimale 'mathématique' de l'entier 9 est 9.

 L'écriture hexadécimale python de l'entier 10 est 0xa.
 L'écriture hexadécimale 'mathématique' de l'entier 10 est a.

 L'écriture hexadécimale python de l'entier 11 est 0xb.
 L'écriture hexadécimale 'mathématique' de l'entier 11 est b.

 L'écriture hexadécimale python de l'entier 12 est 0xc.
 L'écriture hexadécimale 'mathématique' de l'entier 12 est c.

 L'écriture hexadécimale python de l'entier 13 est 0xd.
 L'écriture hexadécimale 'mathématique' de l'entier 13 est d.

 L'écriture hexadécimale python de l'entier 14 est 0xe.
 L'écriture hexadécimale 'mathématique' de l'entier 14 est e.

 L'écriture hexadécimale python de l'entier 15 est 0xf.
 L'écriture hexadécimale 'mathématique' de l'entier 15 est f.

 L'écriture hexadécimale python de l'entier 16 est 0x10.
 L'écriture hexadécimale 'mathématique' de l'entier 16 est 10.

Soit b ≥ 2 un entier. Pour écrire les entiers en base b, on a besoin de b chiffres (qui correspondent aux restes possibles dans une division par b : 0, 1, 2, ..., (b-1)).
Si b ≤ 10, on utilise les symboles usuels pour ces chiffres. Mais si b > 10, on a besoin de nouveaux symboles.

Ainsi la base 16 utilise 16 chiffres : il faut utiliser des symboles désignant les chiffres correspondants à 10_dix, 11_dix, 12_dix, 13_dix, 14_dix, 15_dix (sinon on aurait des ambiguïtés dans les écritures : 12 désigne-t-il le 12 de la base dix ou 1⨯ 16+ 2 ?).

En général, on utilise les lettres (minuscules ou majuscules) a, b, c, d, e, f (pour 10, 11, 12, 13, 14, 15 respectivement).

Passer de l'écriture hexadécimale à l'écriture décimale.

Quelques exemples :

\( 75b3_{\text{seize}}= 3\times 16^0 + 11\times 16^1 +5 \times 16^2 + 7\times 16^3 \)
soit \( 75b3_{\text{seize}}= 30131 \)

\( c00f_{\text{seize}}= 15\times 16^0 + 0\times 16^1 +0 \times 16^2 + 12\times 16^3 \)
soit \( c00f_{\text{seize}}= 49167 \)

Vérifions cela avec python :

print(int(0xc00f))

Réponse de python :

49167

Notations.

On utilisera la notation python (préfixe 0x) ou l'utilisation du mot seize en indice.

Du décimal à l'hexadécimal.

Un théorème.

Tout entier naturel possède une écriture hexadécimale, et une seule.

Et, vous l'avez compris :

Soit b un entier, b ≥2. Tout entier possède une écriture, et une seule, en base b.

La division en cascade

Pour passer de l'écriture décimale à l'écriture hexadécimale, on utilisera bien entendu l'algorithme des divisions en cascade.

Exemple : écrire 3199 en base 16.

D'où 3199= c7f_seize.

L'algorithme est le suivant :

Entrée     :    un entier n.

Traitement :    a ← n
                tant_que a est non nul :
                     r ← reste de la division de a par 16
                     a ← quotient de la division de a par 16
                fin_tant_que
                
Sortie     :    les valeurs successives de r

Il faudra bien sûr penser à remplacer les restes 10, 11, 12, 13, 14, 15 par les symboles a, b, c, d, e, f.

Du binaire à l'hexadécimal et vice-versa.

Du binaire à l'hexadécimal

Comme 16=2⁴, il est possible de passer d'une écriture binaire à une écriture hexadécimale de la façon suivante :

1. On regroupe les bits de l'écriture binaire par paquets de quatre, en ajoutant au besoin des 0 à gauche de l'écriture. Par exemple, N=101011_deux est écrit sous la forme N= 0010   1011.
2. On traduit chaque paquet de quatre en base seize. Avec l'exemple précédent, le paquet 0010_deux s'écrit 2_seize et le paquet 1011_deux s'écrit b_seize.
3. On 'concatène' ces chiffres : on a l'écriture hexadécimale. Ici N=2b_seize.

De l'hexadécimal au binaire.

Si l'on dispose de l'écriture hexadécimale d'un entier N, il suffit d'écrire chacun des chiffres de l'écriture hexadécimale en base deux (sur quatre rang, donc en ajoutant éventuellement des zéros à gauche de chaque traduction de chiffre pour obtenir des paquets de longueur 4) pour obtenir l'écriture en base deux de l'entier N.

Exemple. N=e7_seize. Quelle est l'écriture de N en base 2 ?
On a e_seize=1110_deux et 7_seize=111_deux=0111_deux. D'où N=1110 0111_deux.